こちらの記事では、時系列分析の実装についてまとめています。
時系列分析とは?
時系列分析では、時間経過とともに変化する時系列データを扱います。時系列データの例としては、毎時間の気温、株価の推移等がこれにあたります。売上予測、来店者予測等、ビジネスにおいて重要な分析技術です。
時系列データには以下3種類があります。
1.トレンド
データの長期的な傾向。時間の経過とともに値が上昇・下降している時系列データはトレンドがある、と言えます。
2.周期変動
時間の経過に伴い、データの値が上昇と下降を繰り返すデータのことです。
3.不規則変動
時間の経過と関係なく、値が変動するデータのことを指します。
時系列データが持っている特徴を説明できるようなモデルを構築し、このモデルに基づき予測を行ったり、関連を分析していくことが時系列分析の目的です。時系列分析の際には、時系列データを新しい系列に加工して、それを用いて分析を行います。
加工の主な種類としては、以下4つあります。
1.対数系列
対数変換を行います。数学で習ったlogがこれにあたります。
例えば、10,100,1000といった値を基底10の対数を取れば、log10=1, log100=2, log1000=3と対数変換できます。対数変換するメリットとしては、ばらつきが大きく正規分布をとらないデータを正規分布に近似させることができる点です。
#必要なライブラリをインポートする #対数変換を行う
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
#データを読み込む
# データの読み込み(StatsModelsの検証データを用います)
macrodata = sm.datasets.macrodata.load_pandas().data
macrodata.index = pd.Index(sm.tsa.datetools.dates_from_range("1959q1","2009q3"))
# 読み込んだデータからアメリカの実質GDPの対数変換前の値を表示します。
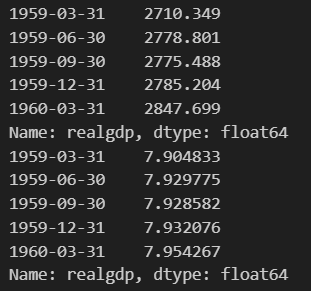
print(macrodata.realgdp.head())
#macrodataを対数変換する
macrodata_realgdp_log = np.log(macrodata.realgdp)
print(macrodata_realgdp_log.head())上5行が対数変換前、下5行が対数変換後の値です。
2.階差系列(差分系列)
時系列データを分析する際、一つ前の時間と値の差を扱うことも多くあります。一つ前の値との差を取ることを差分をとると言い、差分を取った後の系列を階差系列と言います。この変換を行うことにより、トレンドを取り除くことができます(トレンド:大局的に見た時に上昇傾向化、横這いか、下降傾向か)
#必要なライブラリをインポートし、階差系列をとってみる
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import numpy as np
#statsmodelの検証データを読み込む
co2_tsdata = sm.datasets.co2.load_pandas().data
#欠損値の処理
co2_tsdata2 = co2_tsdata.fillna(method="ffill")
#データの階差をとる
co2_tsdata2_diff = co2_tsdata.diff()
#階差前と階差後のグラフを可視化、比較する
plt.subplot(2,1,1)
plt.title("Mauna Loa Weekly Atmospheric CO2 Data")
plt.xlabel("date")
plt.ylabel("CO2 Concentration ppmv")
plt.plot(co2_tsdata2)
plt.subplot(2,1,2)
plt.title("Mauna Loa Weekly Atmospheric CO2 Data DIFF")
plt.xlabel("date")
plt.ylabel("CO2 Concentration ppmv DIFF")
plt.plot(co2_tsdata2_diff)
plt.subplots_adjust(wspace=0, hspace=1.0)
plt.show()上が階差前のグラフ、下が階差後のグラフです。
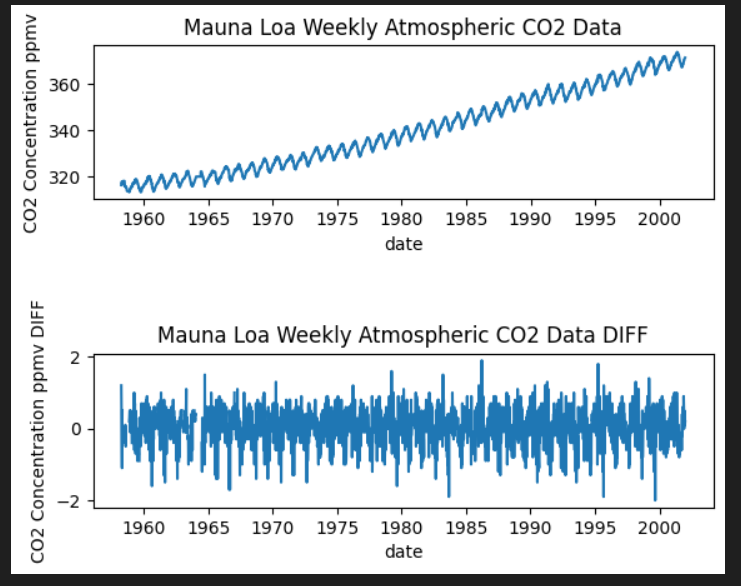
3.季節調整済系列
季節変動が取り除かれたデータを、季節調整済系列と言います。
原系列=トレンド+季節変動+残差と表すことができます。
#季節調整済系列、seasonal_decomposeでトレンド・季節変動・不規則変動に分けることができる
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from numpy import nan as na
import numpy as np
# データの読み込み(StatsModelsの検証データを用います)
co2_tsdata = sm.datasets.co2.load_pandas().data
co2_tsdata2 = co2_tsdata.fillna(method="ffill")
# 季節調整を行い原系列をトレンド、季節変動、残差に分けて出力します
fig = sm.tsa.seasonal_decompose(co2_tsdata2, period=52).plot()
plt.show()StastModelのtsa.seasonal_decompose()を使用することで、現系列をトレンド、季節変動、不規則変動(残差)に分けることができます。
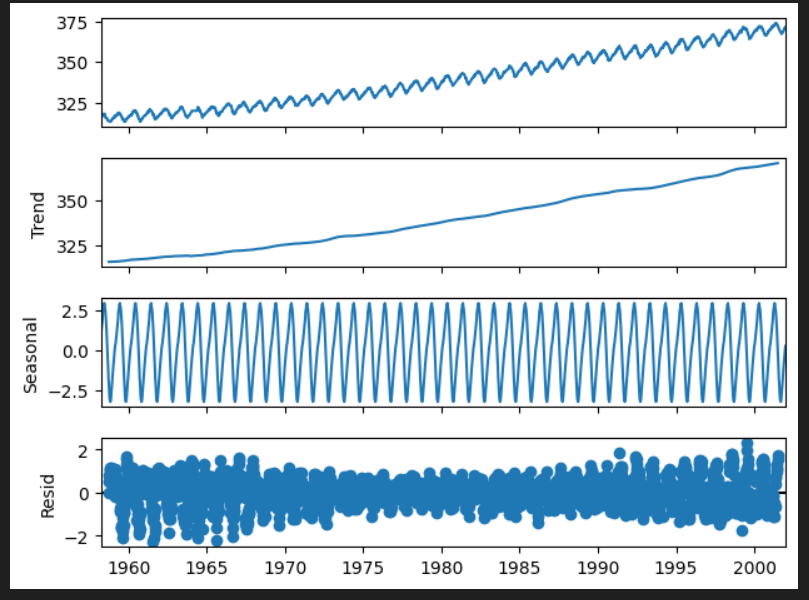
4.移動平均での変換
移動平均とは、時系列データのある一定の区間で平均をとる、ということを区間を移動させながら繰り返すことです。
元データの特徴を残しつつ、データを滑らかにすることができます。移動平均を元の系列から引くことにより、系列のトレンド成分を除去することができます。
#移動平均での変換
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from datetime import datetime
import numpy as np
co2_tsdata = sm.datasets.co2.load_pandas().data
# 欠損値の処理
co2_tsdata2 = co2_tsdata.fillna(method="ffill")
# 原系列のグラフ
plt.subplot(6, 1, 1)
plt.xlabel("date")
plt.ylabel("co2")
plt.plot(co2_tsdata2)
#移動平均を求める
co2_moving_avg = co2_tsdata2.rolling(window=51).mean()
#移動平均のグラフを描画する
plt.subplot(6,1,3)
plt.xlabel("date")
plt.ylabel("co2")
plt.plot(co2_moving_avg)
#原系列-移動平均のグラフを描画する
plt.subplot(6, 1, 5)
plt.xlabel("date")
plt.ylabel("co2")
mov_diff_co2_tsdata = co2_tsdata2-co2_moving_avg
plt.plot(mov_diff_co2_tsdata)
plt.show()一番上が原系列、真ん中が移動平均、下が原系列-移動平均のグラフです。
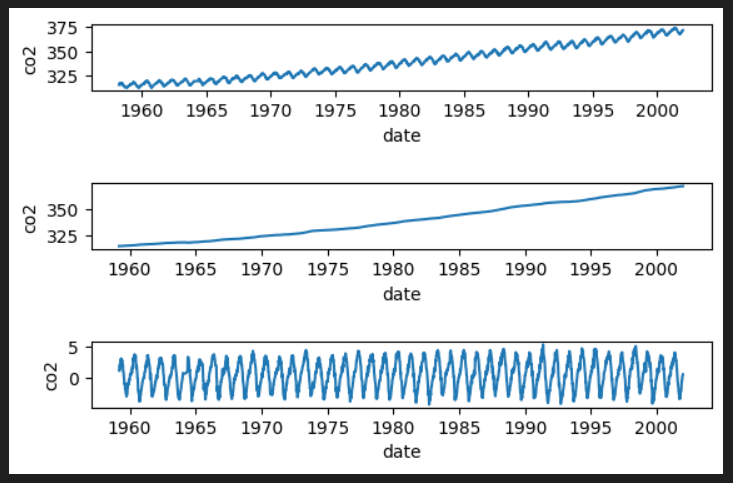
定常性とは?
時系列データを扱う中で、定常性はとても重要な概念です。時系列データの統計的な特性(平均、分散、自己相関など)が時間によらず一定である、つまり時間によって時系列データの構造が変化しない、ということです。
時系列データにおいて定常性がないデータを分析した場合、全く意味のない相関を検出してしまう可能性があるため、定常性のない時系列は上の項目で見たような、対数系列・階差系列・季節調整済系列、移動平均等の変換を行い、定常性を持たせてから分析を進める必要があります。
定常性にも2種類あります。時系列データ分析においては、1の弱定常性を扱う場合がほとんどです。
1.弱定常性
時系列データの期待値と自己共分散(時刻Tのデータが、それよりも前の時刻のデータと相関があるかどうかを示す統計量)が時間を通して一定である、ということです。期待値が一定ということは、時間の経過によらず一定の値に変化しているということ、また自己共分散が一定ということはデータのばらつきが一定ということなので同程度の幅で振れる、ということです。
弱定常性をもつ時系列の例として、ホワイトノイズというものがあります。時点Tによらず、期待値が0、分散が一定、同時点以外の自己共分散を持たないという特徴があります。
2.強定常性
任意の時点、時間差に対して常に同一の同時分布をもつことを指します。
時系列データの分析方法
時系列データを分析するモデルについて、以下のような種類があります。
1.MAモデル(移動平均モデル)
MAモデルはホワイトノイズを拡張したモデルで、過去の誤差を考慮しながらデータ推移の予測をします。たとえばMA(1)は、現在の時刻は一つ前の時刻の誤差の影響を受ける、ということになります。
MAモデル単体としては実際にビジネスに使用されることは少ないですが、MAとARを組み合わせたARIMAモデルやSARIMAモデルが分析で多く使われます。
2. ARモデル(自己回帰モデル)
現在の値を過去のデータを用いて回帰するモデル。失業率や株価の分析に使用されます。
3.ARMAモデル(自己回帰移動平均モデル)
ARモデル(自己回帰モデル)とMAモデル(移動平均モデル)を組み合わせたモデルで、現在の値を過去の値とホワイトノイズによって表現します。ARモデルとMAモデルは互いに競合する性質がないため、組み合わせることが可能です。AR(p)のARモデルとMA(q)のMAモデルを組み合わせた時、ARMA(p, q)と表すことができます。
4.ARIMAモデル(自己回帰和分移動平均モデル)
ARMAモデルへ原系列を階差系列に変換し適応したものをARIMAモデルと言います。ARIMAモデルは定常過程、非定常過程の両方対応可能。
d時点前との差分をとった場合のARMA(p,q)で構築したARIMAモデルを、ARIMA(p,d,q)と表現します。それぞれのパラメータの意味は以下です。
p=自己相関度(モデルが直前p個の値を用いて予測されるか)
d=誘導(時系列データを定常にするためにd次の階差が必要である)
q=移動平均(モデルが直前q個の値に影響を受ける)
5.SARIMAモデル
ARIMAモデルを季節周期をもつ時系列データにも拡張できるようにしたモデルです。(p,d,q)のパラメータに加えて(sp, sd, sq, s)のパラメータを持っています。sp=季節性自己相関、sd=季節性導出、sq=季節性移動平均、s=周期(12か月周期であればs=12)という意味になります。
ARIMAモデルのパラメータ(p, d, q)と基本的な意味は変わりませんが、現在のデータは一つ以上の季節期間を経た過去のデータに影響されます。
これらのパラメータを自動で最適化してくれる機能はないので、情報量基準によってどの値が最も適切なのかを調べるプログラムを書く必要があります。
SARIMAモデルの実装
SARIMAモデルの実装は以下の手順で進めていきます。
1.データの読み込み
2.データの整理(日付の整理、欠損値処理等)
3.データの可視化
4.データ周期の把握(パラメータsの決定)
5.s以外のパラメータの決定
6.モデル構築
7.データと予測の可視化
#必要なライブラリをインポート、データを読み込む
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
url = 'https://www.salesanalytics.co.jp/l6p7'
df_wine = pd.read_csv(url)
#1980年1月から1994年9月までの月次のインデックスを作成し、月毎の頻度を指定。
#生成した日付インデックスを、dw_wineのインデックスにせていし、元のMonthlyの列を削除する
#これらの処理で、月次売上データを扱うデータフレームを準備している
index = pd.date_range("Jan-80","Sep-94",freq="M")
df_wine.index=index
del df_wine["Monthly"]
# 最適なパラメータを算出するため関数の定義
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
# 最適なパラメーターを算出
selectparameter(df_wine,12)
#自己相関、偏自己相関を可視化する
fig=plt.figure(figsize=(12, 8))
# 自己相関係数のグラフを出力します
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_wine, lags=30, ax=ax1)
# 偏自己相関係数のグラフを出力します
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_wine, lags=30, ax=ax2)
plt.show()
#SARIMAモデルを構築する
SARIMA_df_wine = sm.tsa.statespace.SARIMAX(df_wine, order=(0,0,0), seasonal_order=(0,1,0,12)).fit()
#構築したSARIMAモデルのBICを出力します
print(SARIMA_df_wine.bic)
#predに予測データを代入する
pred = SARIMA_df_wine.predict("1994-7-31", "1997-12-31")
#SARIMAで予測したモデルと元のデータの可視化
plt.plot(pred, c="r")
plt.plot(df_wine)
plt.show()以下、解説です。
#必要なライブラリをインポート、データを読み込む
import warnings
import itertools
import pandas as pd
import numpy as np
import statsmodels.api as sm
url = 'https://www.salesanalytics.co.jp/l6p7'
df_wine = pd.read_csv(url)
#月次売上データを扱うデータフレームを準備
index = pd.date_range("Jan-80","Sep-94",freq="M")
df_wine.index=index
del df_wine["Monthly"]必要なライブラリをインポートし、ワインのデータセットを読み込みます。以下のようなデータセットが読み込めました。
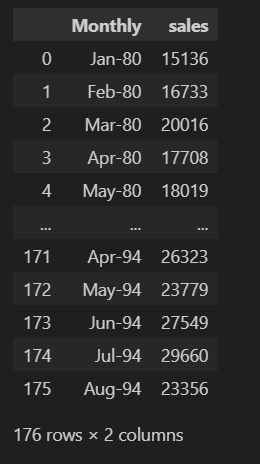
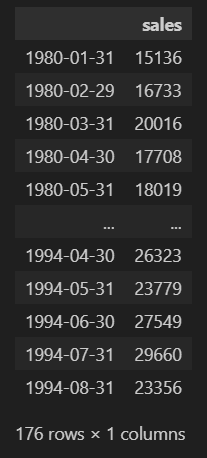
日付の整理を行い、月次売上データを扱うデータフレームを準備します。1980年1月から1994年9月までの月次のインデックスを作成し、月毎の頻度を指定。生成した日付インデックスをdf_wineのインデックスに設定し、元の"Monthly”カラムを削除しました。
# 最適なパラメータを算出するため関数の定義
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
# 最適なパラメーターを算出
selectparameter(df_wine,12)最適なパラメータを算出するため、関数を定義していきます。
def selectparameter(DATA, s)では、selectparameter関数を定義し、データセット"DATA"と季節性周期であるsを引数として受け取ります。
p = d = q = range(0, 2)はARIMAモデルのパラメータ候補として、0-1の範囲で変化するように設定。
pdqでは、intertools.productを使用してパラメータの組み合わせを作成し、pdqに格納しています。intertools.productとはデカルト積を求めることができます。デカルト積とは、各入力イテラブルから一つずつ要素を取り出した全ての組み合わせのことです。
seasonal_pdqでは、季節性のパラメータを含めた組み合わせを作成しています。上記同様、intertools.productでデカルト積を求めていますのですべての組み合わせが格納されます。
parameter/BICSという空のリストを作成し、結果を格納する箱を先に作っておきます。
for文を2回回し、各パラメータに季節性のパラメータ含めた組み合わせを試行します。
sm.tsa.statespace.SARIMAXを使ってSARIMAモデルを構築し、fitでモデルを適合させます。その後、BICを計算しパラメータの組み合わせとBICを先に作成した空のリストに追加していきます。
最後にreturnでBICが最小となる組み合わせを返します。
こちらを実行してみると、以下のような数値が返ってきました。
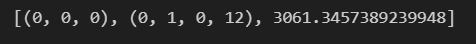
最適パラメータは、p=0, d=0, q=0, sp=0, sd=1, sq=0, s=12となるようです。BICは3061.345...が最小となります。
#自己相関、偏自己相関を可視化する
fig=plt.figure(figsize=(12, 8))
# 自己相関係数のグラフを出力します
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_wine, lags=30, ax=ax1)
# 偏自己相関係数のグラフを出力します
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_wine, lags=30, ax=ax2)
plt.show()
自己相関、偏自己相関を可視化してみます。
sm.graphics.tsa.plot_acfで自己相関をプロット、sm.graphics.tsa.plot_pacfで偏自己相関をプロットします。lags=30は表示するラグの数を指定しています。
自己相関:元のデータとある時点での過去データとの素管を示します。基本的には、データ同士がどれだけ関連しているのかのシンプルな指標です。
偏自己相関:他の時点の影響を除いた、元のデータとある時点での過去データとの純粋な相関を示しています。
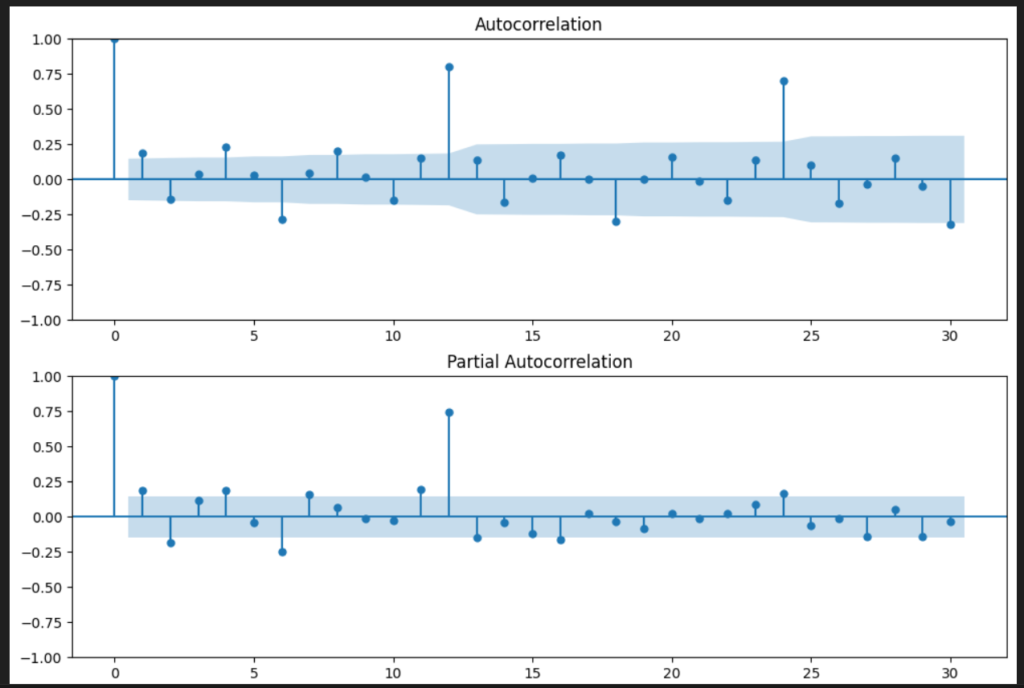
自己相関を見ると、ラグ12,24で0.8と高いので、データには年次の周期性があることがわかります。
#SARIMAモデルを構築する
SARIMA_df_wine = sm.tsa.statespace.SARIMAX(df_wine, order=(0,0,0), seasonal_order=(0,1,0,12)).fit()
#構築したSARIMAモデルのBICを出力します
print(SARIMA_df_wine.bic)
#predに予測データを代入する
pred = SARIMA_df_wine.predict("1994-7-31", "1997-12-31")
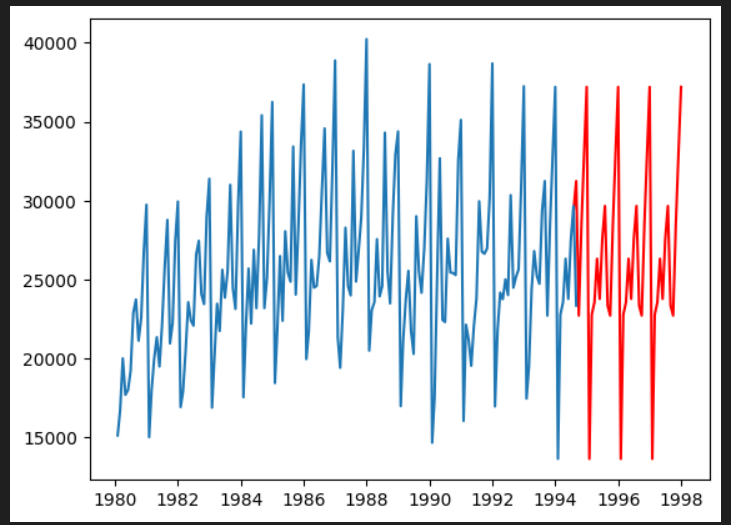
#SARIMAで予測したモデルと元のデータの可視化
plt.plot(pred, c="r")
plt.plot(df_wine)
plt.show()算出した最適なパラメータでSARIMAモデルを構築し、SARIMAで予測したモデルと元データの可視化をしてみます。