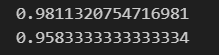こちらの記事では、主成分分析を実装していきます。
Contents
主成分分析とは
主成分分析とは、次元削減を行う時によく使う手法です。例えば、いくつかの特徴量があるデータを2次元データに変換すると、できるだけ情報を保ったまま2軸での描画が可能になり、全てのデータを見やすく示すことができます。
主成分分析の実用例として、製品やサービスのスコアリングや比較(1次元に圧縮)、データの可視化(2,3次元に圧縮)、回帰分析の前処理などが挙げられます。
主成分分析の手順について
主成分分析を使って、通常以下の手順でデータの次元削減を行います。
1.データを標準化する
2.特徴量同士の相関行列を計算する
3.相関行列の固有ベクトルと固有値を求める
4.得られた固有値を大きい方からk個選び、対応する固有ベクトル選択する(k=圧縮したい次元数)
5.k個の固有ベクトルから特徴量行列Wを作成する
6.d次元のデータXと行列Wで行列の積をとり、k次元に変換されたX′ を取得する
sklearn.decomposition のPCAクラスを用いて特徴変換を実装しつつ、ロジスティック回帰を実装していきます。
#ライブラリをインポートする
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
# 指定されたUCIデータセットのIDに基づきデータをダウンロード。Wineのデータセットをダウンロードする
wine = fetch_ucirepo(id=109)
# data (as pandas dataframes)
X = wine.data.features
y = wine.data.targets
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=0)
# 標準化のためのインスタンスを生成
sc = StandardScaler()
# トレーニングデータから変換モデルを学習し、テストデータに適用
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
# 主成分分析のインスタンスを生成
pca = PCA(n_components=2)
# トレーニングデータから変換モデルを学習し、テストデータに適用
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
# ロジスティック回帰のインスタンスを生成
lr = LogisticRegression()
# 次元削減後のトレーニングデータで分類モデルを学習
lr.fit(X_train_pca, y_train.values.ravel())
# スコアの表示
print(lr.score(X_train_pca, y_train))
print(lr.score(X_test_pca, y_test))
解説していきます。
#ライブラリをインポートする
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
# 指定されたUCIデータセットのIDに基づきデータをダウンロード。Wineのデータセットをダウンロードする
wine = fetch_ucirepo(id=109)
# data (as pandas dataframes)
X = wine.data.features
y = wine.data.targets
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=0)まず必要なライブラリをインポートし、ワインのデータセットを読み込みます。
Xに特徴量を、yにラベルを入れます。Xには13の特徴量が入っています。
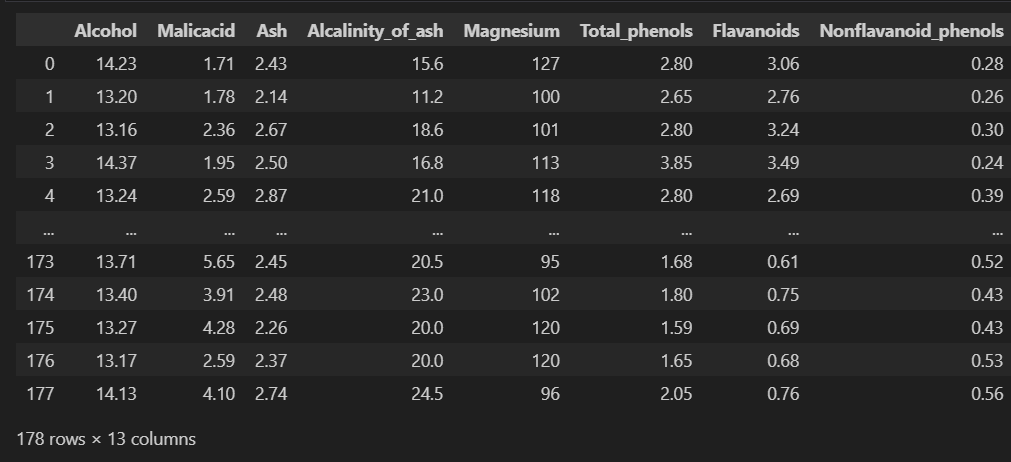
yには以下が入ってます。X, y を訓練データとテストデータに分け、X_train, X_test, y_train, y_testに格納します。
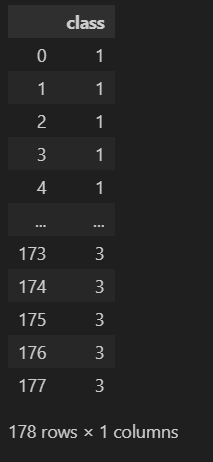
# 標準化のためのインスタンスを生成
sc = StandardScaler()
# トレーニングデータから変換モデルを学習し、テストデータに適用
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)標準化のためのインスタンスを作成し、Xについて訓練データ、テストデータについて標準化を行います。
# 主成分分析のインスタンスを生成
pca = PCA(n_components=2)
# トレーニングデータから変換モデルを学習し、テストデータに適用
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)PCAで主成分分析のインスタンスを作成し、引数のn_componentsで削減後の次元数を指定します。ここでは2次元と指定しています。
標準化したデータを学習し、テストデータに適用させます。
元のXが13次元のデータでしたが、X_train_pcaを確認してみると以下のように2次元に圧縮されていることがわかります。
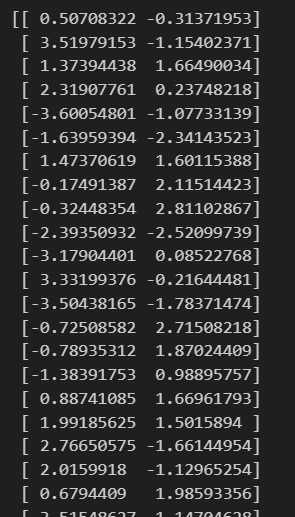
# ロジスティック回帰のインスタンスを生成
lr = LogisticRegression()
# 次元削減後のトレーニングデータで分類モデルを学習
lr.fit(X_train_pca, y_train.values.ravel())
# スコアの表示
print(lr.score(X_train_pca, y_train))
print(lr.score(X_test_pca, y_test))ロジスティック回帰で精度を確認してみます。
ロジスティック回帰のインスタンスを作成し、次元削減後のX_train_pcaを入れ分類モデルを学習させます。
訓練データに対するモデルの精度と、テストデータにたいするモデルの精度を確認します。なかなかいい精度と言えそうです。
13次元から2次元に次元を圧縮しましたが、高い精度を出すことができました。