こちらの記事では、機械学習(教師なし)の非階層的クラスタリング k-means法についてまとめていきます。
Contents
クラスタリングとは
データをクラスター(塊)に分割する操作のことです。クラスタリングの中でも階層的クラスタリングと、非階層的クラスタリングの2種に分けられています。
1.階層的クラスタリング
データの中から最も似ている組み合わせを探し出して、順番にクラスターにしていく方法です。最終的に全データをまとめるクラスターに行くつけば終了です。
2.非階層的クラスタリング
階層的クラスタリングと同様、似ているものをまとめてクラスターを作っていきますが階層構造を持ちません。
データが与えられた際、予めクラスターをいくつ作るかを決定し、その分だけデータからクラスターを作ります。階層構造がないため、計算量が少なく、データ量が多い時に有効な手段です。非階層的クラスタリングの代表的な手法として、k-means法が挙げられます。
k-means法での実装
k-means法は、データを分散の等しいn個のクラスターに分けることができる手法です。各クラスター毎にデータの重心(セントロイド)にあたる平均値が割り当てられます。分散の等しいクラスターに分けるには、SSEという指標を使用します。SSEとは、各クラスターに含まれるデータ点とセントロイドとの2乗和を求めたもの(=分散)です。k-means法は、SSEを全クラスターで等しくかつ最小化するようセントロイドを選びます。
SSEの値が小さいほどクラスタリングがうまくいっているモデルと言えます。
また、k-means法でのクラスター数の決め方として、エルボー法というものがあります。クラスター数を大きくしていった時にSSEがどのように変化するかプロットし、その結果からクラスタ数を決める手法です。出力されるグラフの傾きが急激に曲がる箇所がありますが、この時のクラスタ数を最適とみなします。
それではエルボー法を実施しつつ、k-means法でのクラスタリングを実装してみたいと思います。
#必要なライブラリをインポートする
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.cm as cm
import numpy as np
#sklearn.datasetsのmake_blobs関数をインポートし、データ構造を持っている練習用のデータを準備する
X,Y = make_blobs(n_samples=200, #sサンプル点の数
n_features=2, #特徴量(次元数)
centers=5,#クラスタの個数
cluster_std=0.5,#クラスタ内の標準偏差
shuffle=True, #サンプルをシャッフル
random_state=0 #乱数生成器の状態を指定
)
print(X.shape)
print(Y.shape)
#練習用のデータをプロットする
plt.scatter(X[:, 0],X[:, 1], c="black", marker="*", s=50)
plt.grid()
plt.show()
#エルボー法でk-meansでのクラスターの最適数を決定する
#inertia_でSSEの値を取得する
distortions = []
for i in range (1,11):
km_test = KMeans(n_clusters=i, #クラスターの数
init="random", #初期化手法
n_init=10, #異なる初期中心点を使用したk-menasアルゴリズムの実行回数(10回)
max_iter=300, #各実行での最大反復回数
tol=1e-04, #収束を宣言するための相対的な許容誤差
random_state=0 #乱数生成器の状態を指定
)
km_test.fit(X)
distortions.append(km_test.inertia_)
#グラフのプロットを行う
plt.plot(range(1,11),distortions, marker="o")
plt.xticks(np.arange(1,11))
plt.xlabel("number of clusters")
plt.ylabel("Distortion")
plt.show()
#クラスター数5とし、K-meansクラスからkmインスタンスを作成する
#fit_ptredictでクラスタリングを行う
km = KMeans(n_clusters=5,
init="random", # セントロイドの初期値をランダムに設定 default: "k-means++"
n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数
max_iter=300, # k-meansアルゴリズムを繰り返す最大回数
tol=1e-04, # 収束と判定するための相対的な許容誤差
random_state=0) #乱数発生初期化
Y_km = km.fit_predict(X)
#クラスター番号(Y_km)に応じてデータをプロットする
for n in range(len(Y_km)):
plt.scatter(X[Y_km == n, 0], X[Y_km == n, 1], s=50, c=cm.hsv(
float(n) / 10), marker="*", label="cluster"+str(n+1))
# セントロイドをプロット
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],s=250, marker="*", c="black", label="centroids")
plt.grid()
plt.show()
# クラスタ内誤差平方和にアクセスする
print ("Distortion: %.2f"% km.inertia_)以下、各ブロック毎の説明です。
#必要なライブラリをインポートする
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.cm as cm
import numpy as np
#sklearn.datasetsのmake_blobs関数をインポートし、データ構造を持っている練習用のデータを準備する
X,Y = make_blobs(n_samples=200, #sサンプル点の数
n_features=2, #特徴量(次元数)
centers=5,#クラスタの個数
cluster_std=0.5,#クラスタ内の標準偏差
shuffle=True, #サンプルをシャッフル
random_state=0 #乱数生成器の状態を指定
)
print(X.shape)
print(Y.shape)まず、必要なライブラリをインポートし、sklearn.datasetsのmake_blobs関数をインポートし、データ構造を持っている練習用のデータを準備します。make_blobs関数の引数は上記の通りです。shapeでX,Yのデータの形状を確認してみます。

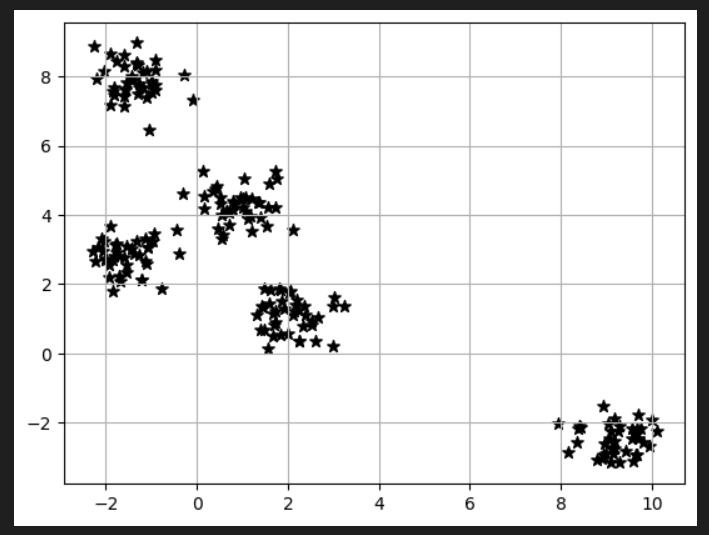
#練習用のデータをプロットする
plt.scatter(X[:, 0],X[:, 1], c="black", marker="*", s=50)
plt.grid()
plt.show()上で作った練習用のデータXを散布図にプロットしてみます。
Xの1列目・全行をx軸に、Xの2列目・全行をy軸としてプロットします。c=色指定、marker=プロットのマーカー形状、s=プロットサイズです。
#エルボー法でk-meansでのクラスターの最適数を決定し、inertia_でSSEの値を取得する
distortions = []
for i in range (1,11):
km_test = KMeans(n_clusters=i, #クラスターの数
init="random", #初期化手法
n_init=10, #異なる初期中心点を使用したk-menasアルゴリズムの実行回数(10回)
max_iter=300, #各実行での最大反復回数
tol=1e-04, #収束を宣言するための相対的な許容誤差
random_state=0 #乱数生成器の状態を指定
)
km_test.fit(X)
distortions.append(km_test.inertia_)クラスター数を1~10まで変化させて、K-meansアルゴリズムを使用し、SSE(歪みの値)をinertia_で取得しdistiortionsに格納しています。
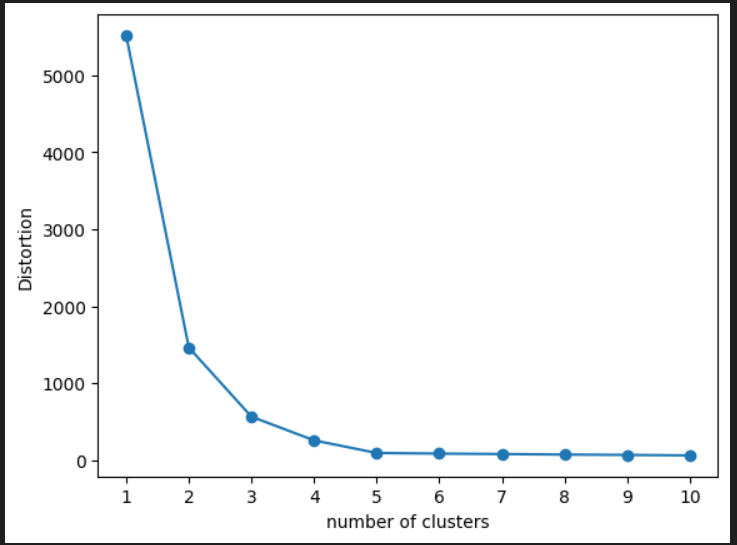
#グラフのプロットを行う
plt.plot(range(1,11),distortions, marker="o")
plt.xticks(np.arange(1,11))
plt.xlabel("number of clusters")
plt.ylabel("Distortion")
plt.show()描画すると以下のようになります。k=5を超えるとクラスタ数を増やしても歪みがほとんど改善しないので、k=5を最適とみなして以下コードを書き進めています。
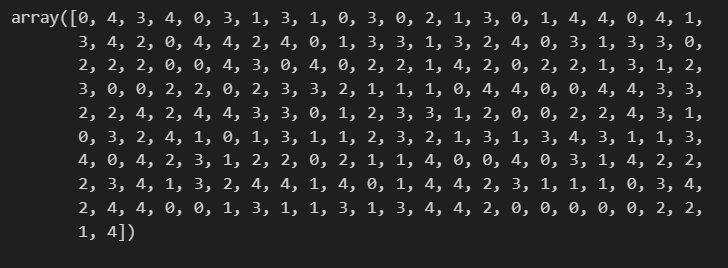
#クラスター数5とし、K-meansクラスからkmインスタンスを作成する
#fit_ptredictでクラスタリングを行う
km = KMeans(n_clusters=5,
init="random", # セントロイドの初期値をランダムに設定 default: "k-means++"
n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数
max_iter=300, # k-meansアルゴリズムを繰り返す最大回数
tol=1e-04, # 収束と判定するための相対的な許容誤差
random_state=0) #乱数発生初期化
Y_km = km.fit_predict(X)エルボー法で決定した最適クラスター数を入れ、K-means法を行います。fit_predictにより、各データポイントがクラスタ番号に割り当てられ、結果がY_kmに返ります。Y_kmには以下が入っています。
#クラスター番号(Y_km)に応じてデータをプロットする
for n in range(len(Y_km)):
plt.scatter(X[Y_km == n, 0], X[Y_km == n, 1], s=50, c=cm.hsv(
float(n) / 10), marker="*", label="cluster"+str(n+1))クラスタ番号に対して、そのクラスタに属するデータポイントのX座標とY座標をプロットします。各クラスタのデータポイントは色とマーカー7の種類が異なるように設定されます。
X[Y_km == n, 0]は、Numpyのインデックスを参照する手法です。ブールインデックス参照と呼ばれる手法を使用して、条件に一致する要素のみを取り出しています。
具体的には、Y_km == nはブールの配列を生成します。ブールの配列は、Y_kmの各要素がnと等しいかどうか示します。このブール配列を使用してXをインデックス参照することで、条件に一致する要素を取り出します。
例として、Xが2次元の配置であり、Y_kmの値が[0,1,1,0,2]であった場合、X[Y_km == 1, 0]は以下のように解釈されます。
Y_km == 1は、[False, True, True, False,False]というブールの配列を生成します。つまり、Y_kmの値が1に等しい要素は2番目と3番目になります。
X[Y_km == 1, 0]はXの各行に対して、Y_kmの値が1に等しい場合にその行の0番目の要素を取り出します。結果、2番目と3番目の行の0番目の要素からなる配列が返ります。
各クラスターのプロットは、cm.hsv(float(n)/10) を使用して設定された異なる色とマーカーの種類を持ちます。
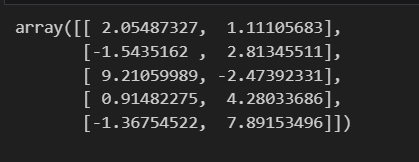
# セントロイドをプロット
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],s=250, marker="*", c="black", label="centroids")
plt.grid()
plt.show()km.cluster_centers_はK-menas法により見つけられたクラスターの中心座標を含む配列です。km.cluster_centers_[:,0]は中心点のX座標を表す配列、km.cluster_centers_[:,1]はY座標を表す配列です。表示させてみると、5つのクラスターの中心点の座標が以下のように入っています。
散布図に描画してみます。
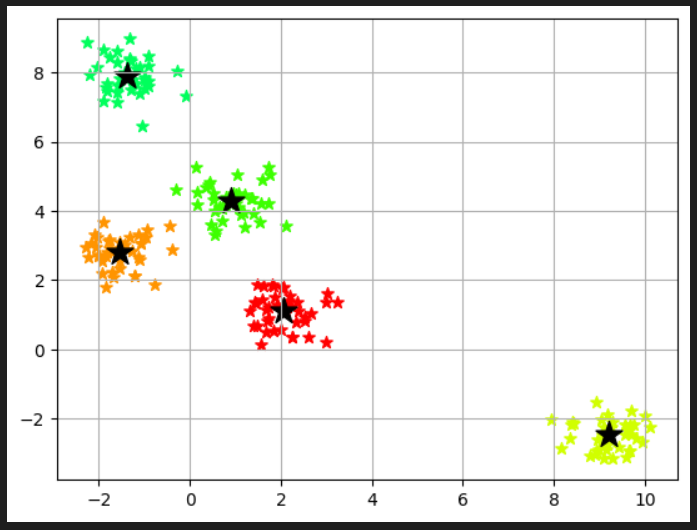
# クラスタ内誤差平方和にアクセスする
print ("Distortion: %.2f"% km.inertia_)クラスタ数5のSSEも出しておきます。