説明変数7つのデータを使用して線形重回帰分析を行ってみます。
※機械学習初学者の勉強のアウトプットですので、もしコードや解釈に間違い等あればご指摘頂けますと幸いです。
Contents
線形回帰とは
説明変数に対して、目的変数が線形またはそれに近い形で表されている状態。
説明変数が1つの場合は単回帰、説明変数が2つ以上の場合は重回帰と呼ばれます。今回実装するのは説明変数が7つの重回帰です。
所得と消費、家賃と部屋の広さ、等、ある一方が他方を左右するという一方向の関係にあるものは回帰分析の手法を取るのが適しています。
線形回帰モデルの実装
#必要なモジュールをインポートする
import urllib.request
import zipfile
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
#既にデータ(sample_data)をダウンロード済の前提
# データの読み込み
sample_data = pd.read_excel("./sample_Data.xls")
#読み込んだデータをテストデータ、検証データに分ける
train_X, test_X, train_y, test_y = train_test_split(
sample_data.drop("Y",axis=1),
sample_data["Y"], random_state=42)
# 線形回帰で回帰分析を行う
model = LinearRegression() #線形回帰の呼び出し
model_fit = model.fit(train_X, train_y) #線形回帰の当てはめ
score_linear = model.score(test_X, test_y) #決定係数算出
y_predict = model.predict(test_X) # テストデータを使って予測を行う
#決定係数を表示
print(f"Linear R2: {score_linear}")
#偏回帰係数を算出
coef = model.coef_
df_coef = pd.DataFrame(coef).T
df_coef.columns = sample_data.columns[:-1]
df_coef.index = ["Estimated coefficients"]
df_coef = df_coef.round(2)
df_coef
#切片を算出
intercept = model.intercept_
intercept
#偏回帰係数をグラフで描画してみる
plt.bar(df_coef.columns, coef)
plt.xlabel("X")
plt.ylabel("Estimated coefficiance")解説
# データの読み込み
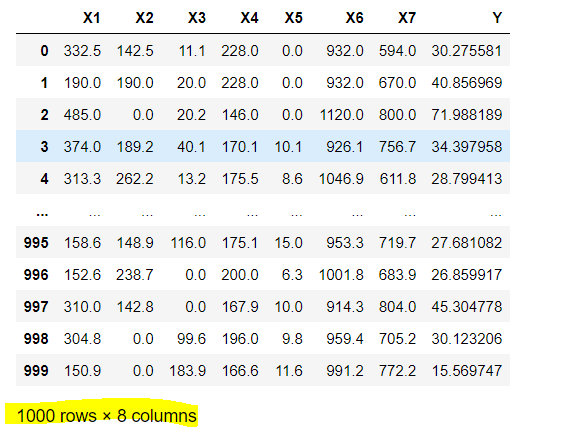
sample_data = pd.read_excel("./sample_Data.xls")ダウンロードして保存したExcelファイルをpd.read_excel("ファイル名")で読み込みます。
読み込んだファイルは以下です。sample_dataで表示させることができます。
今回は1000行×8列(説明変数7+目的変数1)のデータを準備しています。
#読み込んだデータをテストデータ、検証データに分ける
train_X, test_X, train_y, test_y = train_test_split(
sample_data.drop("Y",axis=1),
sample_data["Y"], random_state=42)読み込んだデータをtrain_test_splitでテストデータ、訓練データに分けます。test_size, train_sizeを記載して分割割合を指定することができるが、今回は記載なし=デフォルト値で分析を行っている。デフォルト値は、訓練データ:0.75/ テストデータ:0.25の割合。
train_test_splitの引数であるrandom_stateのデフォルト値はNoneが入っており、Noneのままだとデータのランダムな行が固定されません。つまり、train_test_splitを再実行すると再実行前と異なるtrainデータ、testデータが返されるため、予測結果が都度変わってしまいます。
よってrandom_stateにint型の任意の値を設定して行順番を固定します。
random_stateの値は任意だが、プログラミングで使用される乱数シードは「42」がよく用いられています。全世界で1600万部売れた「銀河ヒッチハイク・ガイド」という書籍の中でこの「42」という数字が出てくるようで、ここからきている模様。
上記の例だと、以下のように分割されます。Xには説明変数、yには目的変数を。今回はY列を求めたいので、これをyに入れます。
・train_X
sample_data.drop("Y",axis=1)、つまりsample_dataから一番右の"Y'列をドロップし、かつ1000行*0.75=750行が格納される
・test_X
train_Xの残りの250行が格納される
・train_y
sample_data["Y"]、つまりsample_dataの'Y'列、かつ1000行*0.75=750行が格納される
・test_y
train_yの残りの250行が格納される
train_Xで中身を確認してみると、sample_dataの一番右の'Y'列がドロップされ、750行が格納されているのが確認できる。

test_yも念のため中身を確認してみると、'Y"列の250行が格納されているのが確認できる。

# 線形回帰で回帰分析を行う
model = LinearRegression() #線形回帰の呼び出し
model_fit = model.fit(train_X, train_y) #線形回帰の当てはめ
score_linear = model.score(test_X, test_y) #決定係数算出
y_predict = model.predict(test_X) # テストデータを使って予測を行うLinearRegression()で線形回帰モデルを呼び出し、model.fit(訓練データX, 訓練データy)で線形回帰モデルを当てはめます。
model.score(テストデータX, テストデータ_y)で決定係数を算出します。
model.predict(テストデータ_X)で、モデルを使用して、Xに対するyの予測値を算出します。
#決定係数を表示
print(f"Linear R2: {score_linear}")決定係数を表示させてみます。
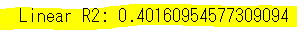
決定係数とは、推定された回帰式の当てはまりの良さを表します。0-1の間で表現され、1に近いほど当てはまりがいい=説明変数が目的変数をよく説明している、ということになります。
様々なページを見ると決定係数が0.5以上だと当てはまりがよいと説明しているものが多いが、絶対的な基準はない模様。
決定係数の平方根=相関係数という関係があるので、例えば0.5の平方根は相関係数0.7となり、強い相関関係があると言えそう。
決定係数0.5はこのような観点から一つの目安となりそうです。
今回の0.4016...の平方根を取ってみると、相関係数0.63となるので、かなり相関関係があると言えます。
#偏回帰係数を算出
coef = model.coef_ #偏回帰係数を算出
df_coef = pd.DataFrame(coef).T #データフレームに変換し転置して説明変数を列にもってくる
df_coef.columns = sample_data.columns[:-1] #サンプルデータの特徴量名称をデータフレームの列名に割当
df_coef.index = ["Estimated coefficients"] #行にEstimated coeffientsラベルを割当
df_coef = df_coef.round(2) #係数を小数点以下2桁にラウンド
df_coef偏回帰係数を算出すると、以下のような結果になります。

そもそも偏回帰係数がなんぞやと言うと、「重回帰分析における変数の係数」と定義されています。
ある一つの変数以外を固定し、その一つの変数を1単位増加/減少した際に、目的変数がどれだけ増加/減少するか」を意味します。
#切片を算出
intercept = model.intercept_
intercept切片を算出すると、以下のようになります。
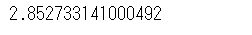
つまり、この重回帰式は以下のように記述できます。
y = (0.11)x1 + (0.08)x2 + (0.07)x3 + (-0.12)x4 + (0.18)x5 + (0.01)x6 + (0.01)x7 + 2.852733...
#偏回帰係数をグラフで描画してみる
plt.bar(df_coef.columns, coef)
plt.xlabel("X")
plt.ylabel("Estimated coefficiance")どの偏回帰係数が影響が大きいかを可視化してみます。
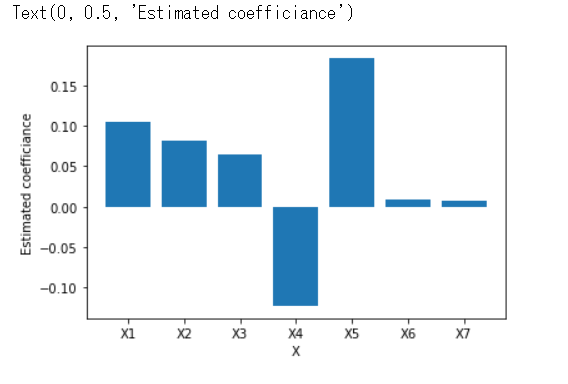
この中だと、X4,X5の影響度が大きいことがわかります。X5の値が大きいとyの値は大きく予測され、一方X4の値が大きいとyの値が小さく予測されます。