こちらの記事では、欠損値の処理について紹介していきます。
欠損値が発生するケースと対応について
機械学習において欠損値がある場合は前処理が必要になります。前処理を行わないと、統計情報が正しく計算できなかったり、適切に分析ができません。
以下のようなケースで欠損値が発生します。
1.MCAR(Missing Completely At Random)
あるデータが欠損する確率がデータと全く無関係である場合。例えば、アンケート結果を記録したファイルが、不具合で欠損値になってしまった場合等があります。
欠損値が無作為に発生しているので、リストワイズ削除(欠損値が含まれるデータ行を全て削除する方法)で処理してもデータに偏りが発生することはありません。ただ、削除することによりデータ件数が大幅に減ってしまう場合は、代入法を使った欠損値の補完を行うこともできます。
2.MAR(Missing At Random)
ある因子が欠損値となるかどうかがその因子自体とは関係ありませんが、その他の因子と関係がある場合。例えば高齢であればあるほど収入に関数データを報告しない(=つまり欠損)が、収入の高さは報告の有無に関係しないといった場合です。
この場合、リストワイズ削除(欠損値が含まれるデータ行を全て削除する方法)で処理をするとデータに偏りがでる可能性があります。観測されたデータから欠損値に入る真の値を予測する代入法で欠損値を補完したほうがよいです。
3.NMAR(Not Missing At Random)
ある項目が欠損する確率がその項目そのものに依存し、その項目以外のデータ項目からもその欠損している項目の欠損率を推測できない場合。例えば、アンケートで年齢が高くなるほど年齢に関して答えなくなり、しかも男性・女性であるかが年齢の欠損には影響しておらず、性別の値からも予測はできない、という場合です。
上述の通り、他のデータ項目からも欠損値を推測できないので、基本的にはデータの再収集を検討する必要があります。
欠損値の代入法について
欠損値の代入法は大きく2種あります。
単一代入法
平均値代入法、確率的回帰代入法、ホットデック法を使って、欠損値を補完して完全なデータセットを1セットだけ作る方法です。
・平均値代入法:欠損しているデータ項目の平均値がわかればいい場合に使います。平均値を持つデータが増える分、対象データ項目の分散が小さくなり、分散や誤差を分析の考慮に入れたい場合は使えません。
・確率的回帰代入法
欠損しているデータ項目の分散をデータ分析で考慮にいれたい場合に使います。
・ホットデック法
質的データが多く、回帰等でパラメトリックに代入値を計算しにくい場合に使用します。
多重代入法
観測されたデータから欠損値を予測して、補完した状態を1セットとし、このセットを複数(=つまり多重)作成し、各セットごとに分析モデルを構築し、個別に構築したモデルを最終的に統合する方法です。
今回は、単一代入法であるホットデック法と、多重代入法を実装してみたいと思います。
ホットデック法の実装
#必要なライブラリをインポートする
import pandas as pd
import numpy as np
import openpyxl
import matplotlib.pyplot as plt
import missingno as msno
import knnimpute as knnimp
#Excelを読みこみ、データと欠損値を確認する
data = pd.read_excel("sampledata.xlsx")
print(data)
data.isnull().sum()
#欠損値を可視化する
msno.matrix(data)
plt.show()
#ホットデック法で欠損値を補完する
matrix = data.values
missing_mask = np.isnan(matrix)
result = knnimp.knn_impute_few_observed(matrix, missing_mask, 3)
pd.DataFrame(result, columns = data.columns)解説
#必要なライブラリをインポートする
import pandas as pd
import numpy as np
import openpyxl
import matplotlib.pyplot as plt
import missingno as msno
import knnimpute as knnimp
#Excelを読みこみ、データと欠損値を確認する
data = pd.read_excel("sampledata.xlsx")
print(data.isnull().sum())
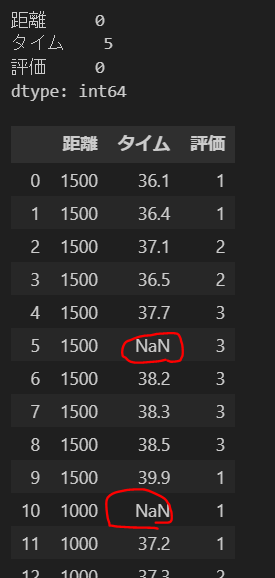
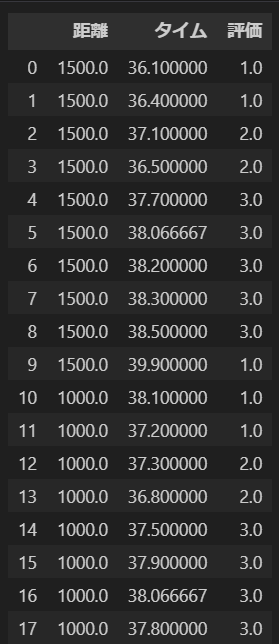
dataまず必要なライブラリをインポートし、サンプルで用意したExcelを読み込み、欠損値を確認します。今回は3カラムのサンプルデータです。
タイムに5つ欠損値があることがわかります。
#欠損値を可視化する
msno.matrix(data)
plt.show()欠損値を可視化してみます。白い部分が欠損値です。
カラム名が日本語だったのでうまく表示されていないようですが、白い部分がある真ん中の列がタイムです。5か所白い部分=欠損値があります。

#ホットデック法で欠損値を補完する
matrix = data.values
missing_mask = np.isnan(matrix)
result = knnimp.knn_impute_few_observed(matrix, missing_mask, 3)
pd.DataFrame(result, columns = data.columns)matrix = data.valuesでdataをNumpyの行列に変換し、"matrix"に代入します。
次に、missing_mask = np.isnan(matrix)でmatrix内の欠損値を検出し、それらの位置に対する要素が"True"であるブール型の行列を作成します。
missing_maskを表示させると以下のようになります。
result = knnimp.knn_impute_few_observed(matrix, missing_mask, 3)で、KNNアルゴリズムを用いて欠損値を補完します。
knn_impute_few_observed関数は、欠損値の数が少ない場合に使用されることが多いです。(欠損値が多い場合には向かない・・・
引数3は補完に使用される最近傍の観測値の数を指定します。
pd.DataFrame(result, columns=data.columns)は、補完された結果をdataFrameに変換し、元のデータフレームと同じカラム名を持つようにしています。中身を確認すると、欠損値が補完できていることがわかります。
多重代入法の実装
#必要なライブラリのインポート
import pandas as pd
import numpy as np
import openpyxl
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.imputation import mice
#Excelを読みこみ、データと欠損値を確認する
data = pd.read_excel("sampledata.xlsx")
print(data)
data.isnull().sum()
#多重代入法で欠損値を補完する
imp_data = mice.MICEData(data)
formula = "評価 ~ タイム + 距離"
#多重代入法のモデルを構築する
model = mice.MICE(formula, sm.OLS, imp_data)
#試行回数3回、データセットの作成は3回という意味
results = model.fit(3,3)
print(results.summary())
#補完した値を含むデータフレームを取得
completed_data = imp_data.data
# 補完されたデータを表示する
print(completed_data)まず必要なライブラリをインポートし、サンプルで用意したExcelを読み込み、欠損値を確認します。今回は3カラムのサンプルデータです。
タイムに5つ欠損値があることがわかります。

#多重代入法で欠損値を補完する
imp_data = mice.MICEData(data)
formula = "評価 ~ タイム + 距離"多重代入法(Multiple Imputation by Chained Equations)を使用して欠損値を補完するための準備を行います。
imp_data = mice.MICEData(data)にて、dataを多重代入法のオブジェクトに変換し、欠損値の補完が可能なデータ形式に整えます。
formula = "評価 ~ タイム + 距離"では、多重代入法のモデル式を指定します。評価を目的変数、タイム・距離を説明変数としてモデルを構築しています。
#多重代入法のモデルを構築する
model = mice.MICE(formula, sm.OLS, imp_data)多重代入法のモデルを構築します。引数として、上で指定したformura式を指定。
sm.OLSは補完に使用されるモデルを指定しています。ここではstatsmodelsの最小二乗法(Ordinaly Least Squares, OLS)を使用しています。
他にも代表的なものとして、一般化線形モデル:sm.GLS(Generalized Linear Model、GLM)、ロバスト線形モデル:sm.RLM(Robust Linear Model、RLM)、重みつき最小二乗法:sm.WLS(Weighted Least Squares、WLS)などがあります。
最後にimp_dataを入れ、これに基づき補完モデルが構築されます。
#多重代入法モデルを実行し、欠損値の補完を行う
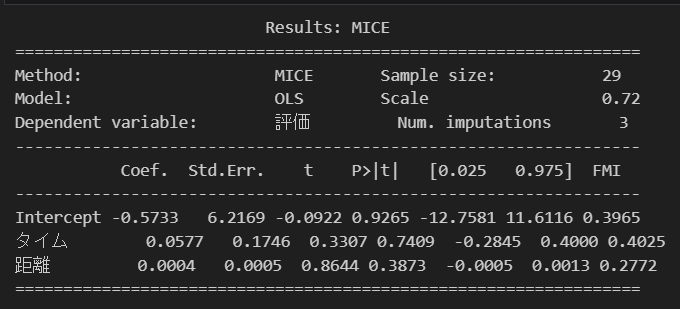
results = model.fit(3,3)
print(results.summary())MICEを三回試行し、データセットを3回作成し、result.summary()で結果の統計量を確認してみます。
#補完した値を含むデータフレームを取得
completed_data = imp_data.data
# 補完されたデータを表示する
print(completed_data)最後にMICEで補完された値を含むデータフレームを取得し、中身を確認してみます。補完できました。