説明変数1つで目的変数を予測する単回帰分析を実装してみたいと思います。
※習初学者の勉強のアウトプットですので、もしコードや解釈に間違い等あればご指摘頂けますと幸いです。
Contents
単回帰分析とは
上述の通り、説明変数1つで目的変数を予測する線形回帰モデル。回帰モデルの基礎です。
単回帰分析の実装
今回はWebサイトの閲覧数と売上のサンプルデータを使用して、単回帰式で分析をしてみたいと思います。
#必要なライブラリのインポート
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
#csvファイルを読み込む
df = pd.read_csv("test.csv",encoding="shift-jis")
print(df.head())
df.shape()
#x, y にそれぞれ説明変数、目的変数を格納する
x = df["売上金額(JPY)"]/1000000 #単位が大きいので1000000で割っておく
y = df["Views"]
#単回帰分析を行う
model = LinearRegression()
model.fit(x.values.reshape(-1, 1), y)
#散布図を描画
plt.plot(x ,y ,"o")
plt.plot(x, model.predict(x.values.reshape(-1, 1)), linestyle="solid")
plt.xticks([50,70,90,110], fontsize=10)
plt.yticks([5000,7000,9000,11000,13000], fontsize=10)
plt.xlabel("Sales(M JPY)",fontsize=10)
plt.ylabel("View",fontsize=10)
plt.show()
#モデルの回帰変数
print('モデル関数の回帰変数 w1: %.3f' % model.coef_)
#モデルの切片
print('モデル関数の切片 w2: %.3f' % model.intercept_)
#モデルの回帰式
print("y= %.3fx + %.3f" %(model.coef_, model.intercept_))
#x,yの相関係数
print("相関係数: %.3f" % x.corr(y))
#モデルの決定係数R2
print("決定係数R2: %.3f" % model.score(x.values.reshape(-1, 1), y))解説
#csvファイルを読み込む
df = pd.read_csv("test.csv",encoding="shift-jis")
print(df.head())
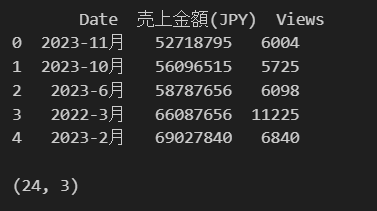
df.shape()保存しているcsvファイルをpd.read_csv("ファイル名")で読み込みます。
読み込んだファイルは以下です。df.head()で最初5行を確認、df.shape()でデータの内容を確認。今回は24行×3列のデータを準備しています。
#x, y にそれぞれ説明変数、目的変数を格納する
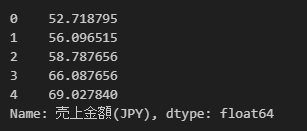
x = df["売上金額(JPY)"]/1000000#単位が大きいので1000000で割っておく
y = df["Views"]x、yにそれぞれ説明変数、目的変数を格納しています。x.head(),y.head()で中身を確認し、それぞれ、以下のように格納できています。
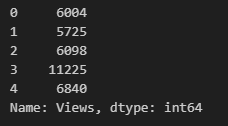
こちらはyの中身です。
#単回帰分析を行う
model = LinearRegression()
model.fit(x.values.reshape(-1, 1), y)LinearRegression()で単回帰モデルを呼び出し、model.fit(訓練データX, 訓練データy)で線形回帰モデルを当てはめる。
この時注意すべきは、.reshape(-1, 1)を用いて次元数を1から2に変更しています。scikit-learnの多くのアルゴリズムが2次元配列を入力として期待するため、、、みたいです。とりあえず単回帰分析の時は、この点注意しようと思います。
#散布図を描画
plt.plot(x ,y ,"o")#説明変数、目的変数を散布図にプロットする
plt.plot(x, model.predict(x.values.reshape(-1, 1)), linestyle="solid")#横軸にx, y軸に単回帰モデルを使用して説明変数xから予測した予測値を入れグラフ描写
plt.xticks([50,70,90,110], fontsize=10)#x軸のメモリ設定
plt.yticks([5000,7000,9000,11000,13000], fontsize=10)#y軸のメモリ設定
plt.xlabel("Sales(M JPY)",fontsize=10)#x軸のラベル設定
plt.ylabel("View",fontsize=10)#y軸のラベル設定
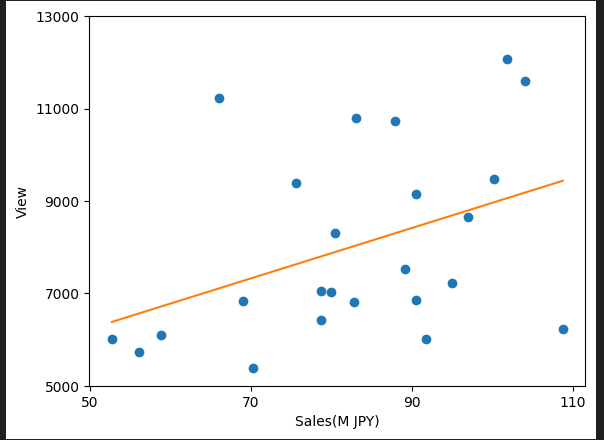
plt.show()散布図と回帰直線は以下のようになります。でも、これだけでは関係あるのかパッと見わかりにくいです。
回帰式を算出、相関係数や決定係数を見てみたいと思います。
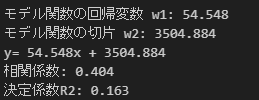
#モデルの回帰変数
print('モデル関数の回帰変数 w1: %.3f' % model.coef_)
#モデルの切片
print('モデル関数の切片 w2: %.3f' % model.intercept_)
#モデルの回帰式
print("y= %.3fx + %.3f" %(model.coef_, model.intercept_))
#x,yの相関係数
print("相関係数: %.3f" % x.corr(y))
#モデルの決定係数R2
print("決定係数R2: %.3f" % model.score(x.values.reshape(-1, 1), y))%.3fの意味ですが、%:フォーマット文字列の開始、.3:小数点以下の桁数、f:不動小数点数、を表します。
print('モデル関数の回帰変数 w1: %.3f' % model.coef_)を例でとると、不動小数点model.coefの値が、小数点以下3桁で表されることになります。
以下が結果です。相関係数0.404ということなので、説明変数xと目的変数yの間にはやや相関がある、決定係数R2は0.163なので回帰式の当てはまりはよくない、という結果になりました。