機械学習(教師あり学習 分類)の非線形SVMを実装してみたいと思います。
※学習初学者の勉強のアウトプットですので、もしコードや解釈に間違い等あればご指摘頂けますと幸いです。
メモも兼ねて、各コードなるべく詳しく説明をつけるようにしています。
前提:教師あり学習 分類とは?
カテゴリ別に分けてあるデータを学習し、未知のデータのカテゴリを予測する手法です。
新商品をメールで案内する時に、顧客の過去の購買履歴を使用し購買見込みが高い人を予測、その人のみに特別なメールを送る、などの活用例があります。
分類は大まかに2項分類、多項分類に分けられます。
2項分類:YES/ NOのように、予測するカテゴリが2つの分類を指します。さらに線形分類・非線形分類に分けられます。
多項分類:分類するカテゴリが3つ以上の分類を指します。
分類の主な手法について
・ロジスティック回帰:
線形分離可能なデータの境界線を見つけ、データの分類を行う手法。境界が直線になるので、2項分類等カテゴリの少ないデータの分類に使用される。「回帰」とあるが分類の手法であることに注意。
・線形SVM(サポートベクターマシン):
データの境界線を見つけ、線形分類を行う手法。SVMはサポートベクトルというベクトルを用いて境界線を引きます。SVMは境界線が2カテゴリの最も離れた場所に引かれるので、ロジスティック回帰よりも一般化されやすく精度が高い傾向があります。
・非線形SVM(サポートベクターマシン):
線形SVMの”線形分離可能なデータ"しか分類できない、という欠点を補うために開発されたモデルです。
・決定木:
データの説明変数(要素)に注目し、説明変数内のある値を堺にデータを分割し、データの属するカテゴリを決定する手法。
それぞれの説明変数が目的変数にどの程度の影響を与えているのかを見ることができます。分割を繰り返して枝分かれしていくが、先に分割される条件に用いられる変数ほど、影響力が高いと言えます。線形分離できないデータは分類が難しい点が欠点。
・ランダムフォレスト:
決定木を複数作り、分類の結果を多数決で決める手法。アンサンブル学習の手法の一つ。
決定木では、全ての説明変数を使用していたが、ランダムフォレストでは少数の説明変数を用いてデータのカテゴリを決定します。
線形分離できない複雑なデータでも分類可能。
・k-NN:
k近似法とも呼ばれる。予測するデータと類似したデータを見つけ、多数決により分離結果を決める手法。
教師データから学習するのではなく、教師データを直接参照してラベルを予測するのが他の分類手法との違い。k-NNの特徴としては、学習コストが0である点、アルゴリズムが単純だが比較的精度が高い点、複雑な形の境界線も表現可能な点が挙げられます。
非線形SVMの実装
今回はskleranのirisデータセットを使用して、非線形SVMを実装していきます。
4つの特徴量(sepal length(cm): がく片の長さ/sepal width(cm): がく片の幅/petal length(cm): 花びらの長さ/petal width(cm): 花びらの幅)とラベル(0: setosa/1:versicolor/2:virginica)で構成されているデータセット(150件)です。
本コード内で、非線形SVMと線形SVMの比較も行ってみます。
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import LinearSVC
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn import metrics
#アヤメのデータセットを取得し、中身を確認する
iris = datasets.load_iris()
#irisデータセットの全行と0列目、2列目をXに格納する
X = iris.data[0:, [0,2]]
#yにtargetを格納する
y = iris.target
#train_data ,testデータに分割し、分割できているか確認
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = 0.3, random_state=42)
print(f"train_X:{train_X.shape}")
print(f"test_X:{test_X.shape}")
print(f"train_y:{train_y.shape}")
print(f"test_y:{test_y.shape}")
#モデルを構築する
model1 = SVC()
model2 = LinearSVC()
#モデルに学習させる
model1.fit(train_X, train_y)
model2.fit(train_X, train_y)
#test_Xとtest_yを用いて正答率を出す
print(f"Non Linear SVM score: {model1.score(test_X, test_y)}")
print(f"Linear SVM score: {model2.score(test_X, test_y)}")
#matplotlibで可視化を行う、図を作成する
fig, (axL, axR) = plt.subplots(ncols=2, figsize=(10,4))
#非線形SVMの散布図を描画する
axL.scatter(X[:, 0], X[:, 1], c=y, marker=".", cmap=matplotlib.cm.get_cmap(name="cool"), alpha=1.0)
#モデルが学習した決定境界をプロットしていく
#特徴空間の範囲を指定する、0列目の特徴量、1列目の特徴量の最小値-1と最大値+1を指定し、特徴空間の範囲を広げておく
x1_min, x1_max = X[:, 0].min() - 1 , X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1 , X[:, 1].max() + 1
#徴空間をメッシュグリッドで表現する
#x1_min,x1_maxまでの範囲を0.02刻みで配列を作成する
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02), np.arange(x2_min, x2_max, 0.02))
#学習済モデル(model1)を使用し、各座標のラベルを予測する
Z1 = model1.predict(np.array([xx1.ravel(), xx2.ravel()]).T).reshape(xx1.shape)
#contourfで等高線を作成し、alphaで透明度、cmapでカラーマップを指定する
axL.contourf(xx1, xx2, Z1, alpha=0.4, cmap=matplotlib.cm.get_cmap(name="Wistia"))
#描画する際の表示範囲設定、タイトルをつける
axL.set_xlim(xx1.min(), xx1.max())
axL.set_ylim(xx2.min(), xx2.max())
axL.set_title("classification data using SVC")
axL.set_xlabel("Sepal length")
axL.set_ylabel("Petal length")
axL.grid(True)
#線型SVMを描画する
axR.scatter(X[:, 0], X[:, 1], c=y, marker=".", cmap=matplotlib.cm.get_cmap(name="cool"), alpha=1.0)
x1_min, x1_max = X[:, 0].min() - 1 ,X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1 ,X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02), np.arange(x2_min, x2_max, 0.02))
Z2 = model2.predict(np.array([xx1.ravel(), xx2.ravel()]).T).reshape(xx1.shape)
axR.contourf(xx1, xx2, Z2, cmap=matplotlib.cm.get_cmap(name="Wistia"), alpha=0.4)
axR.set_xlim(xx1.min(), xx1.max())
axR.set_ylim(xx2.min(), xx2.max())
axR.set_title("classification data using LinearSVC")
axR.set_xlabel("Sepal length")
axR.grid(True)
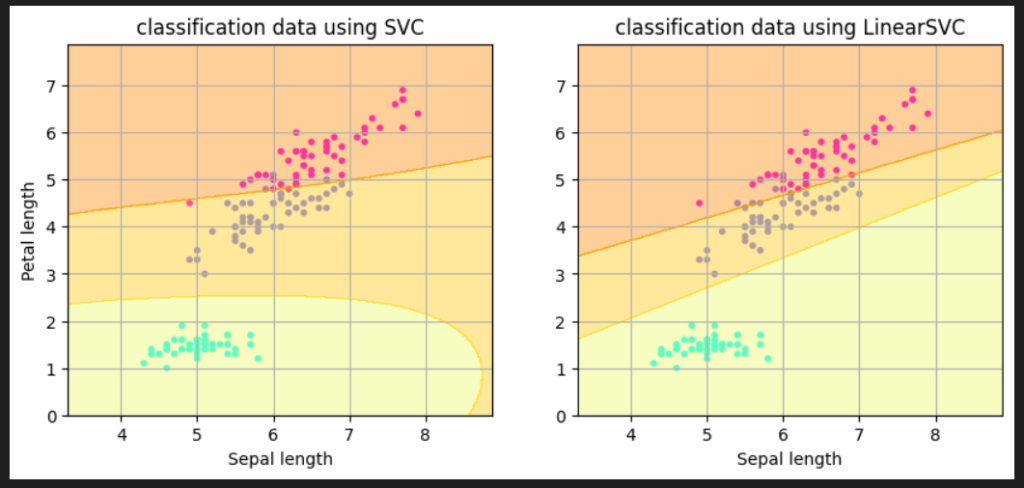
plt.show()解説
#irisデータセットを取得し、中身を確認する
iris = datasets.load_iris()
iris.keys()必要なライブラリをインポートした後、irisのデータセットを読み込みます。
iris.keys()で、key値が取得できます。

たとえば、iris.feature_namesとすると、特徴量の名称が確認できます。
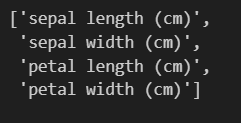
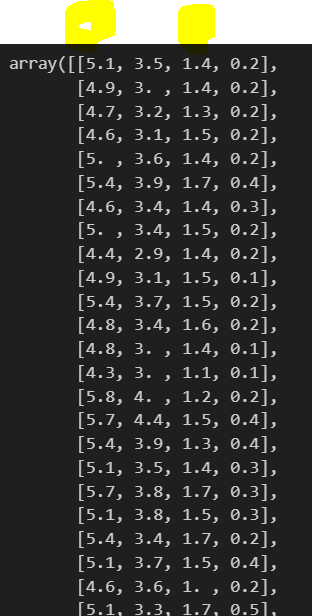
#irisデータセットの全行と0列目(sepal length)、2列目(petal length)をXに格納する
X = iris.data[0:, [0,2]]元々のirisのデータの中身をiris.dataで確認してみると、以下のようになります。
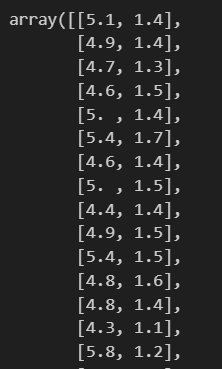
そこから黄色で色をつけた0列目、2列目をXに格納します。
iris.data[0:, [0,2]]で、0:全行、[0,2]で0列目と2列目を指定しています。中身を確認すると、以下のように格納できていることがわかりました。
#yにtargetを格納する
y = iris.targetyにtarget(ラベル)を格納していきます。ラベルが格納されていることも確認できました。

#train_data ,testデータに分割し、分割できているか確認
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = 0.3, random_state=42)
print(f"train_X:{train_X.shape}")
print(f"test_X:{test_X.shape}")
print(f"train_y:{train_y.shape}")
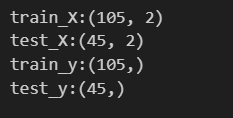
print(f"test_y:{test_y.shape}")trainデータ(0.7)とtestデータ(0.3)に分割し、分割できているかを念のため確認しておきます。
元々データセットは150件だったので、train_X: 105行×2列、test_X: 45行×2列、train_y: 105行×1列、test_y: 45行×1列となっていれば大丈夫です。念のため.shapeで確認しておきます。
#モデルを構築する
model1 = SVC()
model2 = LinearSVC()
#モデルに学習させる
model1.fit(train_X, train_y)
model2.fit(train_X, train_y)
#test_Xとtest_yを用いて正答率を出す
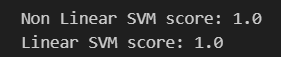
print(f"Non Linear SVM score: {model1.score(test_X, test_y)}")
print(f"Linear SVM score: {model2.score(test_X, test_y)}")model1を非線形SVM、model2を線形SVMとします。
それぞれ、train_X、train_yを入れて学習させ、.score()でtest_X、text_yを入れて正答率を出します。正答率100%です。
#matplotlibで可視化を行う、図を作成する
fig, (axL, axR) = plt.subplots(ncols=2, figsize=(10,4))figは図全体を表すオブジェクトです。(axL, axR)はサブプロットを表すオブジェクトのタプルです。
ncols=2により2列をもつサブプロットが作成されます。左のサブプロットはaxL、右のサブプロットはaxRと定義されます。
figsizeで図のサイズを指定、この場合は幅が10インチ、高さが4インチとなります。
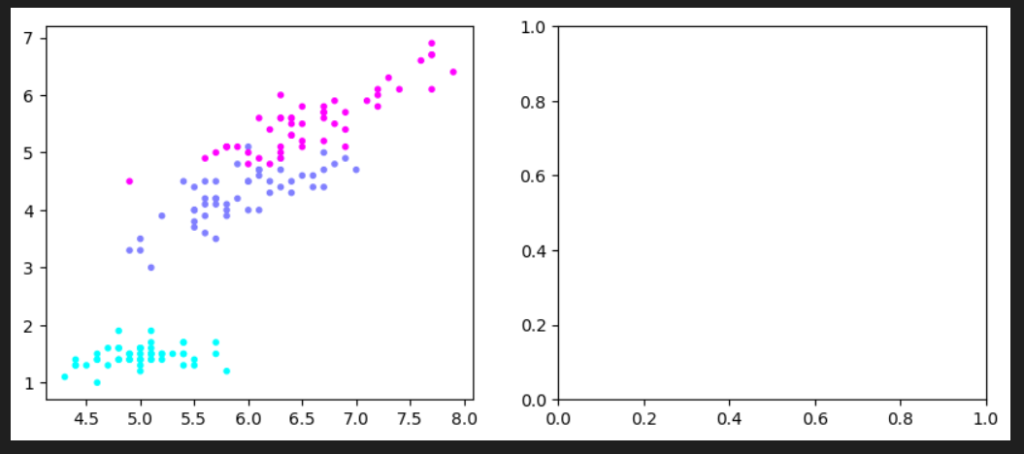
#非線形SVMの散布図を描画する
axL.scatter(X[:, 0], X[:, 1], c=y, marker=".", cmap=matplotlib.cm.get_cmap(name="cool"), alpha=1.0)まず、axLに非線形SVMの散布図を描画していきます。X軸とY軸の値を指定し、他のパラメーターも調整します。
#モデルが学習した決定境界をプロットしていく
#特徴空間の範囲を指定する、0列目の特徴量、1列目の特徴量の最小値-1と最大値+1を指定し、特徴空間の範囲を広げておく
x1_min, x1_max = X[:, 0].min() -1, X[:, 0].max() +1
x2_min, x2_max = X[:, 1].min() -1, X[:, 1].max() +1特徴空間の範囲をまず指定します。例えば、X[:, 0].min()-1の意味は、Xに格納した全行、0列目の中で一番小さい値を抽出。特徴空間の範囲を広げるため、-1をしておきます。
#特徴空間をメッシュグリッドで表現する
#x1_min,x1_max/x2_min,x2_maxまでの範囲を0.02刻みで配列を作成する
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02),
np.arange(x2_min, x2_max, 0.02))meshgridは格子点を作る関数です。基本的な考え方はこちらのサイトを参考にさせて頂きました。とてもわかりやすいです。
x1_min,x1_max/x2_min,x2_maxまでの範囲を0.02刻みで配列を作成し、それぞれxx1, xx2に格納していきます。
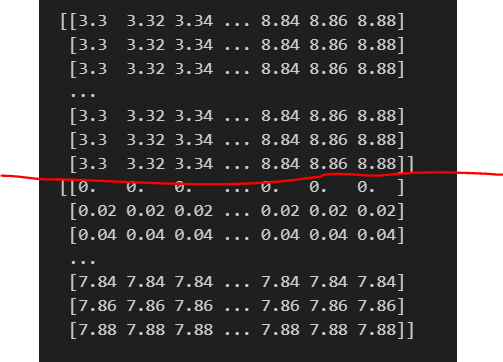
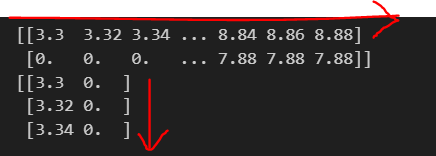
print()で表示してみると、以下のようになります。
赤線より上がxx1(X軸の値), 下がxx2(Y軸の値)の値になります。(3.3, 0), (3.32, 0), (3.34, 0), ・・・(8.84, 0), (8.86, 0), (8.88, 0),と言った格子点です。
shape()で確認すると、xx1/xx2ともに(395, 280)の配列であることがわかります。
#学習済モデル(model1)を使用し、各座標のラベルを予測する
Z1 = model1.predict(np.array([xx1.ravel(), xx2.ravel()]).T).reshape(xx1.shape)学習済モデルを使用し、各格子点のラベルを予測していきます。
予測する際にはデータを一次元に戻す必要がありますので、ravel()でxx1, xx2をそれぞれ1次元配列に戻します。1次元配列に戻すと、(110600, )となります。元の配列が395×280 =110600なので、正しく一次元配列に戻りましたが、今は列方向に配列が並んでいるので.Tで転置して行方向に配列が並ぶようにします。転置をしないと"X has 110600 features, but LogisticRegression is expecting 2 features as input."というエラーがでます。
一次元に戻したものを学習済モデルに入れ、各格子点のラベルを予測します。
その後、予測したラベルを元々のxx1の配列(395, 280)の形にreshape()で戻します。
#contourfで等高線を作成し、alphaで透明度、cmapでカラーマップを指定する
axL.contourf(xx1, xx2, Z1, alpha=0.4, cmap=matplotlib.cm.get_cmap(name="Wistia"))
#描画する際の表示範囲設定、タイトルをつける
axL.set_xlim(xx1.min(), xx1.max())
axL.set_ylim(xx2.min(), xx2.max())
axL.set_title("classification data using SVC")
axL.set_xlabel("Sepal length")
axL.set_ylabel("Petal length")
axL.grid(True)contourfは等高線を引く時に使います。contourf(格子点のX座標の配列、格子点のY座標の配列、値の配列)として値を渡します。
今回は、xx1、xx2、そしてxx1/xx2から予測したラベルの値をそれぞれ渡します。
cmapでカラーマップの色を指定します。Matplotlibのサイトで確認できます。Alphaは透明度を調整します。
最後に、描画する際の表示範囲を指定、グラフにタイトルをつけます。非線形SVMの描画完了です。
同様に以下コードで線形SVMを描画していきます。
#線型SVMを描画する
axR.scatter(X[:, 0], X[:, 1], c=y, marker=".", cmap=matplotlib.cm.get_cmap(name="cool"), alpha=1.0)
x1_min, x1_max = X[:, 0].min() - 1 ,X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1 ,X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02), np.arange(x2_min, x2_max, 0.02))
Z2 = model2.predict(np.array([xx1.ravel(), xx2.ravel()]).T).reshape(xx1.shape)
axR.contourf(xx1, xx2, Z2, cmap=matplotlib.cm.get_cmap(name="Wistia"), alpha=0.4)
axR.set_xlim(xx1.min(), xx1.max())
axR.set_ylim(xx2.min(), xx2.max())
axR.set_title("classification data using LinearSVC")
axR.set_xlabel("Sepal length")
axR.grid(True)
plt.show()以下のように描画できました。