こちらの記事では、機械学習(教師なし)の非階層的クラスタリング DBSCAN法についてまとめていきます。
Contents
クラスタリングとは
データをクラスター(塊)に分割する操作のことです。クラスタリングの中でも階層的クラスタリングと、非階層的クラスタリングの2種に分けられています。
1.階層的クラスタリング
データの中から最も似ている組み合わせを探し出して、順番にクラスターにしていく方法です。最終的に全データをまとめるクラスターに行くつけば終了です。
2.非階層的クラスタリング
階層的クラスタリングと同様、似ているものをまとめてクラスターを作っていきますが階層構造を持ちません。
データが与えられた際、予めクラスターをいくつ作るかを決定し、その分だけデータからクラスターを作ります。階層構造がないため、計算量が少なく、データ量が多い時に有効な手段です。
DBSCANでの実装
DBSCANは、クラスターの高密度の場所を低密度の場所から分離して捉えます。クラスターの大きさ・形に偏りがあるデータ場合に有効です。
DBSCANでは、eps(あるデータの半径)とmin_samples(データ数)の指標を用いて、以下3点にデータをわけます。
1.あるデータの半径eps内にmin_samples数だけのデータがある場合、そのデータ点はコア点とみなす
2.コア点ではないが、コア点から半径eps内に入っているデータはボーダー点とする
3.どちらも満たさない場合はノイズと判定される
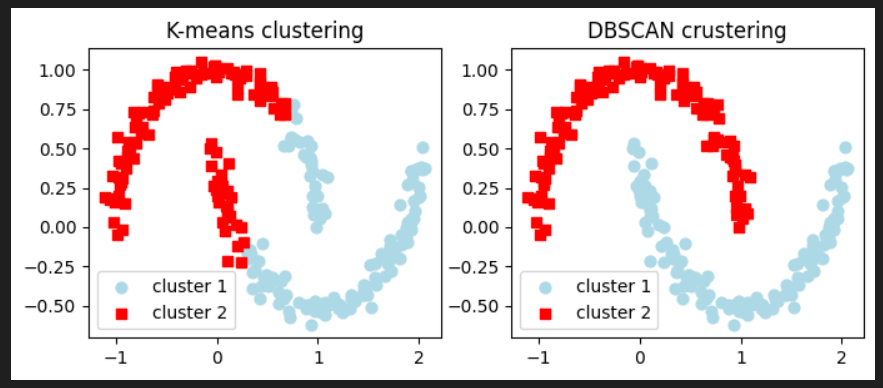
DBSCANでのクラスタリングを実装しつつ、クラスタリング結果をk-means法とも比較してみたいと思います。
#必要なライブラリをインポートする
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.cm as cm
import numpy as np
#sklearn.datasetsのmake_moons関数をインポートし、月型のデータ構造を持っている練習用のデータを準備する
#上向き、下向きの弧が相互に噛み合う形で生成され、直線では分離できないデータセットを準備する
X,Y = make_moons(n_samples=250, #サンプル点の数
noise = 0.05, #ばらつきを付与
random_state=0 #乱数生成
)
#グラフを定義
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))
#k-means法でクラスタリングを行う
km = KMeans(n_clusters=2, random_state=0)
Y_km = km.fit_predict(X)
ax1.scatter(X[Y_km == 0, 0], X[Y_km == 0, 1], c="lightblue",
marker="o", s=40, label="cluster 1")
ax1.scatter(X[Y_km == 1, 0], X[Y_km == 1, 1], c="red",
marker="s", s=40, label="cluster 2")
ax1.set_title("K-means clustering")
ax1.legend()
#DBSCANでクラスタリングを行う
db = DBSCAN(eps=0.2, min_samples=5, metric="euclidean")
Y_db = db.fit_predict(X)
ax2.scatter(X[Y_db == 0, 0], X[Y_db == 0, 1], c="lightblue",
marker="o", s=40, label="cluster 1")
ax2.scatter(X[Y_db == 1, 0], X[Y_db == 1, 1], c="red",
marker="s", s=40, label="cluster 2")
ax2.set_title("DBSCAN crustering")
ax2.legend()
plt.show() まず、必要なライブラリをインポートし、sklearn.datasetsのmake_moons関数をインポートし、月型のデータ構造を持っている練習用のデータを準備します。make_moons関数の引数の意味は上記の通りです。shapeでX,Yのデータの形状を確認してみます。
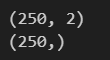
#グラフを定義する。
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))plt.subplotを使用して、1行2列のレイアウトを持つ図を作成します。
fは図全体を管理するためのオブジェクトで、これを使用することにより図全体のレイアウトを設定したり、複数のサブプロットを配置できます。
#k-means法でクラスタリングを行う
km = KMeans(n_clusters=2, random_state=0)
Y_km = km.fit_predict(X)
ax1.scatter(X[Y_km == 0, 0], X[Y_km == 0, 1], c="lightblue",
marker="o", s=40, label="cluster 1")
ax1.scatter(X[Y_km == 1, 0], X[Y_km == 1, 1], c="red",
marker="s", s=40, label="cluster 2")
ax1.set_title("K-means clustering")
ax1.legend()K_means法でクラスタリングを行いax1に描画します。K_means法については、以下の記事で別途まとめています。
X[Y_km == 0, 0]は、Numpyのインデックスを参照する手法です。ブールインデックス参照と呼ばれる手法を使用して、条件に一致する要素のみを取り出しています。
具体的には、Y_km == 0 はブールの配列を生成します。ブールの配列は、Y_kmの各要素が0と等しいかどうか示します。このブール配列を使用してXをインデックス参照することで、条件に一致する要素を取り出します。
例として、Xが2次元の配置であり、Y_kmの値が[0,1,1,0,2]であった場合、X[Y_km == 1, 0]は以下のように解釈されます。
Y_km == 1は、[False, True, True, False,False]というブールの配列を生成します。つまり、Y_kmの値が1に等しい要素は2番目と3番目になります。
X[Y_km == 1, 0]はXの各行に対して、Y_kmの値が1に等しい場合にその行の0番目の要素を取り出します。結果、2番目と3番目の行の0番目の要素からなる配列が返ります。
#DBSCANでクラスタリングを行う
db = DBSCAN(eps=0.2, min_samples=5, metric="euclidean")
Y_db = db.fit_predict(X)
ax2.scatter(X[Y_db == 0, 0], X[Y_db == 0, 1], c="lightblue",
marker="o", s=40, label="cluster 1")
ax2.scatter(X[Y_db == 1, 0], X[Y_db == 1, 1], c="red",
marker="s", s=40, label="cluster 2")
ax2.set_title("DBSCAN crustering")
ax2.legend()
plt.show() 次にDBSCANでax2に描画していきます。eps = クラスタの範囲を表すパラメータ、min_samples =クラスターとみなすために必要な最小データポイント数、metric=距離計算に使用されるメトリックです。今回ハユークリッド距離を指定しています。
K-means とDBSCANで描画すると以下のようになりました。
の非階層的クラスタリング DBSCAN法についてまとめていきます。 Contents1 クラスタリングとは2 DBSCANでの実装 クラスタリングとは データをク){kind=link}